Scientific Measurements . . . . Recording the Significant Numbers
1. When recording a digitally displayed number on a laboratory instrument, write down every displayed number. If a balance displays 1.520 grams, write 1.520 grams . . . not 1.52 grams . . . the trailing zero is significant.
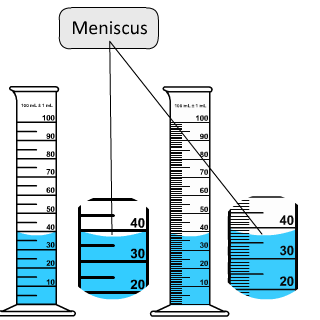
2. When determining a value from lab glassware, for example the volume of water in a graduated cylinder, you should estimate the water's position to one decimal place past the markings - read from the bottom of the . . . . menisci, from Greek, meaning crescent is a distinct curvature at an aqueous solution's upper surface when placed in a glass buret. The solvent (water) is attracted to the glass and is pulled up the glass causing the curvature in the center of the tube.
A meniscus is not observed when the material is plastic..
- The cylinder on the left is marked to the tens / fives place and read to the ones place . . . . the estimated reading is 38 mL
- The cylinder on the right is marked to the ones place and read to the tenths place . . . . the estimated reading is 37.2 mL
Scientific Calculations . . . . Reporting the Significant Numbers

You perform a chemistry lab and collect "lab data". After the lab, you submit a lab report that contains your lab data, lab calculations and results / conclusions. On your first lab calculation, your calculator displays the answer as 23.456546987532. You wonder . . . .
Are all these numbers necessary?
Many scientists asked this same question until the German mathematician Carl Friedrich Gauss developed the following rules for determining which numbers are significant in a calculated number.
After lab data has been recorded to the maximum number of significant digits, use the rules to the left to determine the number of significant figures in the numbers calculated from your lab data and any needed chemistry constants.

Student entering lab data
and chemistry constants into her
calculator and recording the
answer to the correct number of
significant figures.
Rules For Determining Significant Figures |
|||||||||
| 1. All non-zero numbers (1, 2, 3, 4, 5, 6, 7, 8, 9) are ALWAYS significant. | 125.3 contains 4 SigFigs | ||||||||
| 2. All zeros between non-zero numbers are ALWAYS significant. | 1000.3 contains 5 SigFigs | ||||||||
| 3. All zeros that are to the right of a decimal point AND at the end of the number are ALWAYS significant. | 1.300 contains 4 SigFigs 0.00290 contains 3 SigFigs |
||||||||
| 4. All zeros that are to the left of a written decimal point AND are in a number greater than or equal to 10 are ALWAYS significant. | 9800. contains 4 SigFigs 8600 contains 2 SigFigs |
||||||||
|
|
|||||||||
Significant Figures Rules For Addition / Subtraction When adding or subtracting numbers, count the number of decimal places (DP) to determine the number of significant figures. The answer cannot contain more places after the decimal point than the smallest number of decimal places in the numbers that are added or subtracted.26.11548 (5 DP) + 1.2587 (4 DP) + 0.21 (2 DP) = __________ Your Calculator will report the answer as 27.58418 You should report the answer to 2 DP . . . . 27.58418 If the number to the right of the 8 (e.g. the 4) is a 5 or greater, "round up" the 8 The correct reporting of the answer is 27.58 (2 DP . . . 4 SF) or 2.758E1 (. . . . the first non-zero digit has a "." to its right. If the absolute value of the number is ≥ 10 or < 1, it will have "E" followed by a non-zero number. For example, 0.000345 is written as 3.45E-4 in scientific notation.) Significant Figures Rules For Multiplication / Division When multiplying or dividing numbers, count the number of significant figures (SF) in each number used. The answer cannot contain more significant figures than the number being multiplied or divided with the least number of significant figures.2611.548 (7 SF) × 1.2593 (5 SF) × 0.210 (3 SF) = __________ Your Calculator will report the answer as 690.631703 You should report the answer to 3 SF . . . . 690.631703 If the number to the right of the 0 (e.g. the 6) is a 5 or greater, "round up" the 0 The correct reporting of the answer is 691 (3 SF) or 6.91E2 |
|||||||||
Activity: use the significant figure rules above to determine the number of significant figures in the numbers and calculated answers displayed below. Answer 9 questions correctly to display the Tutorial Complete message.
Accuracy and Precision - accurate results are those whose average value is close to the true or accepted value. Precise results are those where the individual results are close to each other.
