Chemistry, like all sciences, uses tools that report measured values in metric units. Knowing that femto (f) is 10-15 is the first step in creating a conversion factor and using it in a calculation.
But what does a femtometer (fm) equal?
- Is 1 fm = 1E15 m?
- Is 1E-15 fm = 1 m?
- Is 1 fm = 1E-15 m?
- Is 1E15 fm = 1 m?
Two answers are correct, but which two? The problem you may be experiencing is that these are "numbers on a page" . . . non-scientists do not routinely encounter units like "femto" or "pico". None of us would be confused with "is it 3 feet in a yard . . . or 3 yards in a foot".
There's got to be a way to be correct 100% of the time in Chemistry . . . . THERE IS . . . . check out the Conversion Factor column below.
| Prefix |
Symbol |
Factor |
Conversion Factor |
|
| femto |
f |
10-15 |
To make an equality, always place the " 1 " in front of the prefix and the number representing the prefix on the other side of the equation. For example:
1 fm = 1E-15 m
Dividing both sides by 1E-15 m gives
1 fm
1E-15 m |
= |
1E-15 m
1E-15 m
|
|
1 fm
1E-15 m |
= |
1 |
|
| pico |
p |
10-12 |
| nano |
n |
10-9 |
| micro |
μ |
10-6 |
| milli |
m |
10-3 |
| centi |
c |
10-2 |
| deci |
d |
10-1 |
| kilo |
k |
103 |
| mega |
M |
106 |
| giga |
G |
109 |
| tera |
T |
1012 |
Activity: complete the TRQ 1.4a: Metric Prefixes assignment.
| If |
1 fm
1E-15 m |
= 1, then |
1E-15 m
1 fm |
= 1 |
Now, we have two conversion factors for the same equality, 1 fm = 1E-15 m.
Let us use the first one to convert 1.234E-2 m into fm.
1.234E-2 m
|
× |
1 fm
1E-15 m
|
= |
1.234E13 fm |
Mathematically, we have multiplied 1.234E-2 by 1 . . . so, we have not changed it. The two numbers (1.234E-2 m and 1.234E13 fm) look different, but they are the same length.
Similarly, 5280 feet, 1760 yards and 1 mile look different, but they are the same length.
Now let's use the second conversion factor above to convert 1.234E16 fm into m.
1.234E16 fm
|
× |
1E-15 m
1 fm
|
= |
1.234E1 m |
Activity: Complete the TRQ 1.4b: Conversion Factors and Units and TRQ 1.4c: Conversion Factors and Units assignments so this information is "available" when solving dimensional analysis problems.
- 453.6 graham crackers = 1 pound cake
- Time between slipping on a peel and smacking the pavement = 1 bananosecond
- Weight an evangelist carries with God = 1 billigram
- Half a large intestine = 1 semicolon
- 1,000,000 aches = 1 megahurtz
- 10 cards = 1 decacard
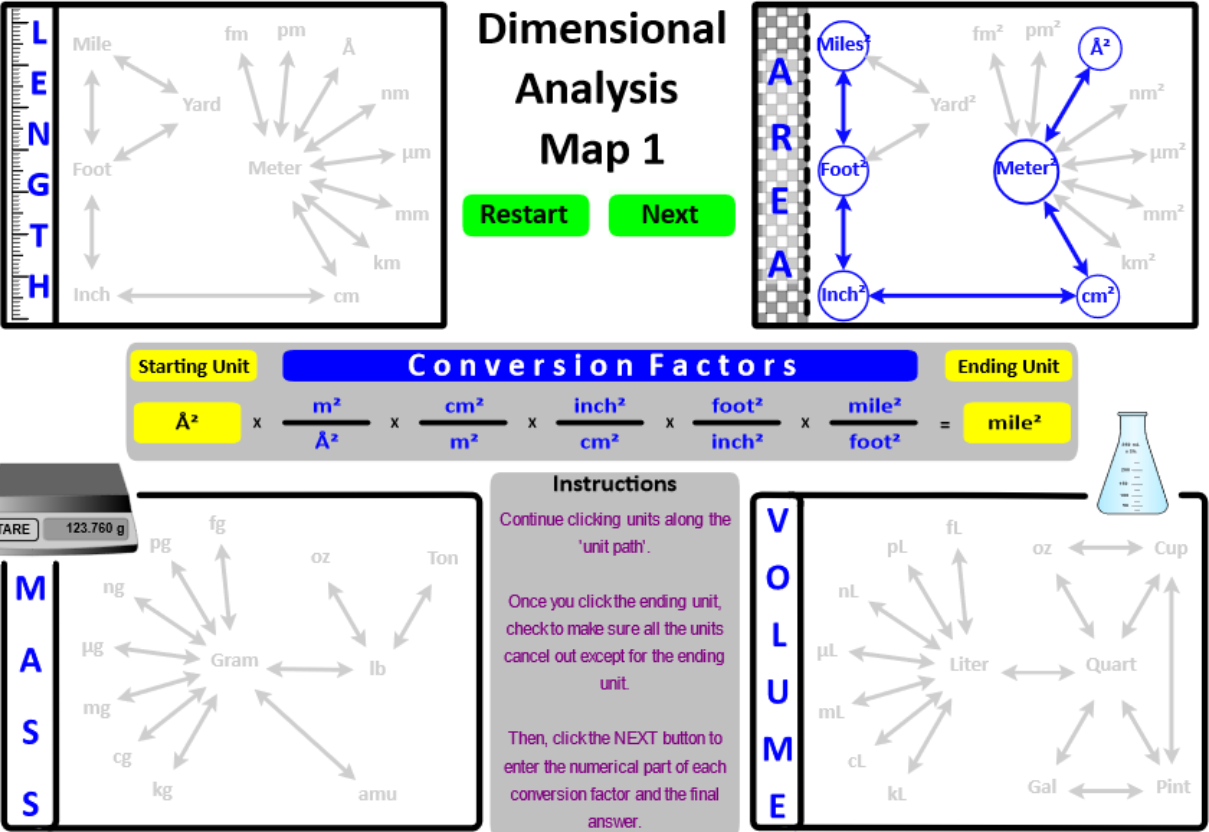
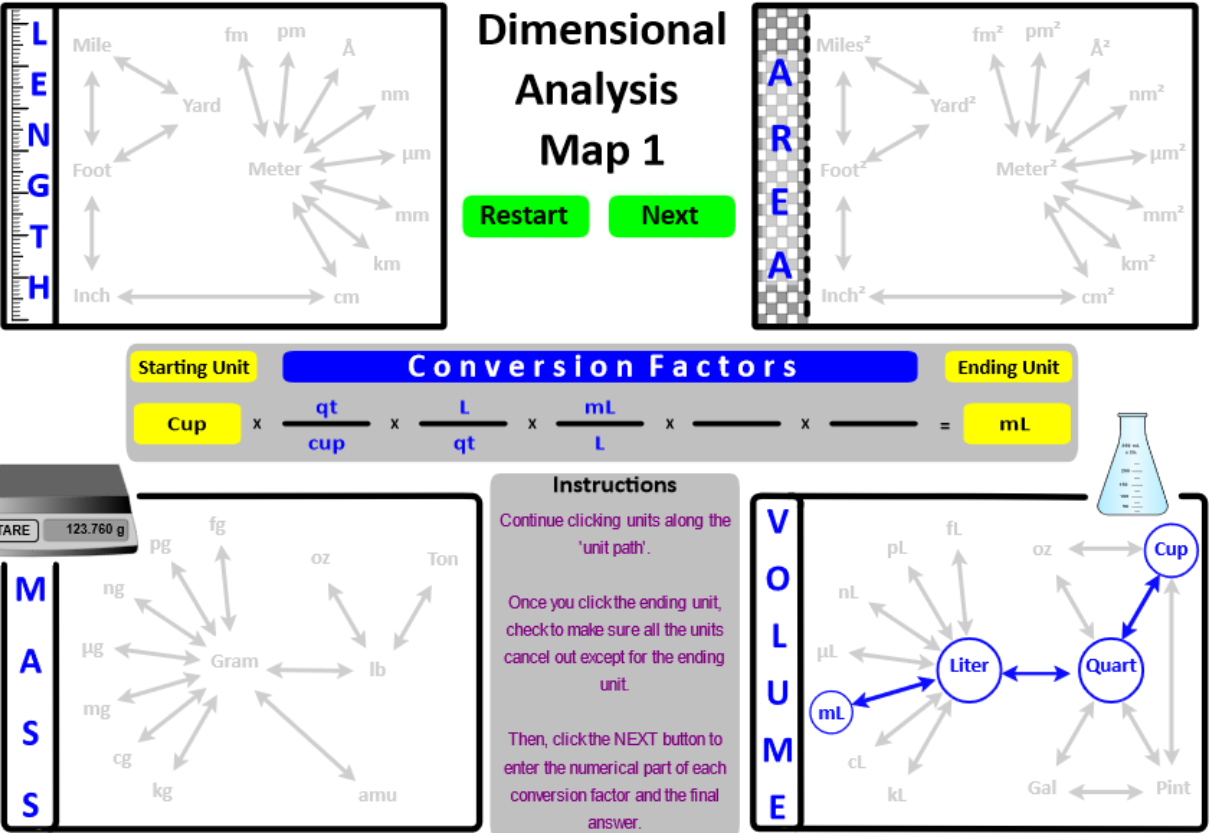
One-step and two-step conversions are relatively simple . . . . like driving to the local grocery store - only one or two turns. However, for multi-step calculations (i.e. a "road-trip") a map is essential. Students use a Dimensional Analysis Map to give them an overview of the "roads" they will use to arrive at a calculation's destination.
The English and Metric units of length, area, mass, and volume are "connected" in the Dimensional Analysis Map 1 (below). This interactive map provides a visual overview of the factor-unit method when converting a measurement from one unit to a different unit.
In a text book, the conversion of 23.4 yards to femtometers is presented as . . . .
23.4 yds
|
× |
3 ft
1 yd
|
× |
12 in
1 ft
|
× |
2.54 cm
1 in
| × |
1E-2 m
1 cm
| × |
1 fm
1E-15 m
|
= |
2.14E16 fm |
This "five-step" journey is visually represented in the "Length" image below.
Activity: complete the HW 1.4a: Dimensional Analysis Map 1 and HW 1.4b: Dimensional Analysis Map 1 assignments. Open the assignment and click the Work Problem link. Create a path from the starting unit to the ending unit as described in the activity above. Then, click the Next button to open a webpage where you will enter the numbers associated with each unit as shown in the textbook example above. Calculate the answer. Finally, mouse over the TOL link to see the tolerance used to grade your answer. Typically, this is set to +/- 0 in a certain significant figure. If . . . . the first non-zero digit has a "." to its right. If the absolute value of the number is ≥ 10 or < 1, it will have "E" followed by a non-zero number. For example, 0.000345 is written as 3.45E-4 in scientific notation.is required, enter your calculated answer to the specified tolerance and in scientific notation . . . click the Submit button.
"You have to 'ball-park' your numbers" . . . . a memorable quote from my college chemistry professor, Dr. McPherson.
Should you trust your Calculator? Absolutely!! The chance that it computes an answer incorrectly is extremely small . . . . it is the data input specialist that you always need to double-check.
How do you "ball-park" the answer to a calculation? Add and subtract the exponents (powers of 10) to see if the calculator's answer is close to (in the ball park) of your estimated magnitude. If you estimate the magnitude of your answer as 10000 (105 or 1E5) and your calculator says the answer is 0.24576 . . . . something's wrong.
1E2 × 1E-6 = 1E-4 . . . . add exponents when multiplying . . . . +(2) +(-6) = -4
1E2 ÷ 1E-6 = 1E8 . . . . subtract exponents when dividing . . . . +(2) -(-6) = 8
1E-12 × 1E-2 ÷ 1E-4 = 1E-10 . . . . add exponents when multiplying, subtract exponents when dividing . . . . +(-12) +(-2) -(-4) = -10
Activity: practice predicting the value of the exponent in the following problems. Once you have written down an answer, click Show Answer to check your answer.
|
|
|
|
|
|
|
|
|
|
|
| 1E3 |
× |
1
1E-6 |
× | 1E3
1 |
× | 1
1E-9 |
= |
Show Answer
+(3) -(-6) +(3) -(-9) = E21
|
| 1E‑13 |
× |
1E-2
1 |
× | 1E3
1 |
× | 1E9
1 |
= |
Show Answer
+(-13) +(-2) +(3) +(9) = E-3
|
| 1E-6 |
× |
1
100 |
× |
1
1E-9 |
× |
1
1E-15 |
× | 1
1000 |
= |
Show Answer
+(-6) -(2) -(-9) -(-15) -(3) = E13
|
|
|
= |
Show Answer
+(-3) -(9) – [-(-6) +(3)] = E-21
| Alternatively, when presented with a fraction divided by a fraction, you can mentally "invert and multiply" the fractions in the denominator . . . . |
|
1E-3
1 |
× |
1
1E9 |
× |
1E-6
1 |
× |
1
1E3 |
|
| +(-3) -(9) +(-6) -(3) = E-21 |
|
|
|
|
| |
Activity: complete the TRQ 1.4d: Estimating Powers assignment to enhance your . . mental calculations . .
. . computational estimations . .
. . problem solving . . .
Activity: Mouseover the sphere, cube, and cylinder to display the formulas used to calculate their volumes.
Density is the ratio of the mass of a sample to its volume. The typical units for density depend on the state of matter:
- Solids and liquids have units of g/mL or g/cm3 or g/cc (1 mL = 1 cm3 and a "cc" is a cubic centimeter)
- Gases have units of g/L (since the mass of hydrogen gas is much smaller than an equal volume of a solid or liquid, chemists prefer to write the density of hydrogen gas as 0.08988 g/L instead of 0.00008988 g/mL)
The activity to the left demonstrates that the volume of regularly-shaped objects are calculated from one or two measurements.
Volume and Water Displacement
Suppose you can't find your ruler or you are given an irregularly-shaped object . . . . no worries. It turns out that the volume of any object equals the volume of water that it displaces when submerged.
In the 3rd century B.C., Archimedes measured the volume of an irregularly-shaped object using what later became known as the . . . . a submerged object displaces its volume of liquid . . . . a floating object displaces its weight of liquid King Hiero II tasked him to determine if his new crown was made out of pure gold. While sitting in a bath, he had a . . . . or Aha! moment refers to the common human experience of suddenly understanding a problem or concept that had previously eluded comprehension.
The translation of Eureka is "I have found it!" . . . literally the first one. He discovered that the volume of an object equals the volume of water it displaces.
Activity: Determine the density of the metal cylinder in the interactive lab animation to the right.
- Tare the balance - click the TARE button . . . . the balance reads 0.000 g
- Click, drag, and drop the metal cylinder onto the tared balance
- Click, drag, and drop the metal cylinder into the graduated cylinder
- The density is calculated by dividing the mass of the metal cylinder by the volume of the metal cylinder. The volume of the metal cylinder is determined by subtracting the graduated cylinder's starting volume from its final volume.
- Identify the metal in the animation. Open the interactive Periodic Table and mouse over the metals (Al, Ti, Cu, Zn, Pt, Au, and Pb) to display their densities (top, middle). Compare these densities to the density calculated for metal cylinder in the animation. Identify the metal element in the cylinder . . . . to check your answer, mouseover the element symbols below.
Incorrect ✘
DensityAl = 2.698 g/mL Incorrect ✘
DensityTi = 4.507 g/mL Correct ✓
DensityCu = 8.96 g/mL Incorrect ✘
DensityZn = 7.14 g/mL Incorrect ✘
DensityPt = 21.45 g/mL Incorrect ✘
DensityAu = 19.28 g/mL Incorrect ✘
DensityPb = 11.34 g/mL
Activity: complete the Lab 1.4a: The Scientific Method Part 2 assignment. This virtual lab continues using the scientific method to investigate the cause of the dramatic reduction in mass of the US penny in 1982.
Activity: complete the Lab 1.4b: Density of Solids and Liquids assignment. In addition to determining the density of two liquids and two solids, this lab contains a virtual component similar to the animation above where you will use density to identify an unknown metal.
Activity: complete the TRQ 1.4e: Lab Equipment assignment. Both hands-on labs and virtual labs (like Lab 1.4b) use scientific equipment and recognizing / naming this equipment is an essential skill that you must develop.