| Mass percent = | Mass of component
Mass of solution |
× 100% |
Mass Percentage
Mass percentage is defined as the component's mass ÷ the solution's mass × 100%.
| Parts per million = | Mass of component
Mass of solution |
× 106 |
In dilute solutions, the mass percent can be a small number that is better expressed in the units of parts per million (ppm). For example, the [K+]sea water is 0.038 % which is 380 ppm or 380 mg/L. The ppm formula is very similar to the mass percent formula . . . . except 100 is replaced by 1,000,000 (or 106).
| Parts per billion = | Mass of component
Mass of solution |
× 109 |
Ions like lead (Pb2+) can cause serious health issues in very dilute solutions (> 15 ppb or > 15 µg/L). The equation for calculating parts per billion (ppb) is the same as the ppm equation except 106 is replaced with 109.
Volume Percentage
| Volume percent (v/v %) = | Volume of component
Volume of solution |
× 100% |
| 70% Rubbing alcohol = | 70 mL IPA
100 mL solution |
× 100% |

Volume percentage is used when a solution is created by combining two liquids. Volume percent (v/v%) is defined as the component's volume ÷ the solution's volume × 100%. Rubbing alcohol is 70% isopropyl alcohol (IPA) . . . . every . . . . 100 mL solution is chosen because it cancels out with the 100% in the formula to the right. This makes the volume of the component equal to the percent (70% for rubbing alcohol) contains 70 mL of pure isopropyl alcohol.
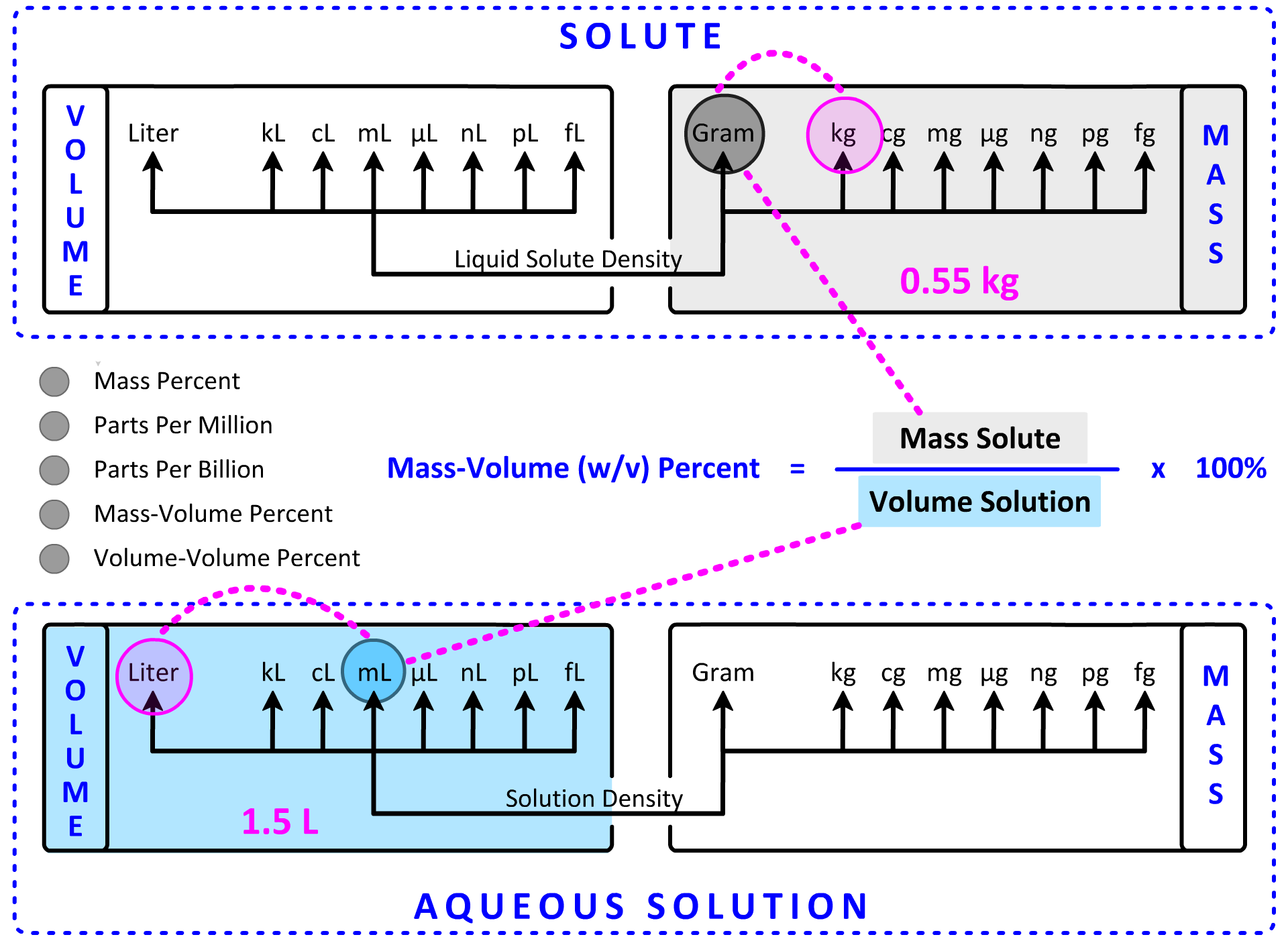
Mass-Volume Percentage
| Mass-Volume percent (m/v %) = | Mass of component
Volume of solution |
× 100% |
| 0.9% Physiological saline = | 0.9 g NaCl
100 mL solution |
× 100% |

Mass-Volume percentage units are popular for pharmaceutical and medical applications. The 0.9 % (m/v) physiological saline solution contains 0.9 g sodium chloride per 100 mL solution.
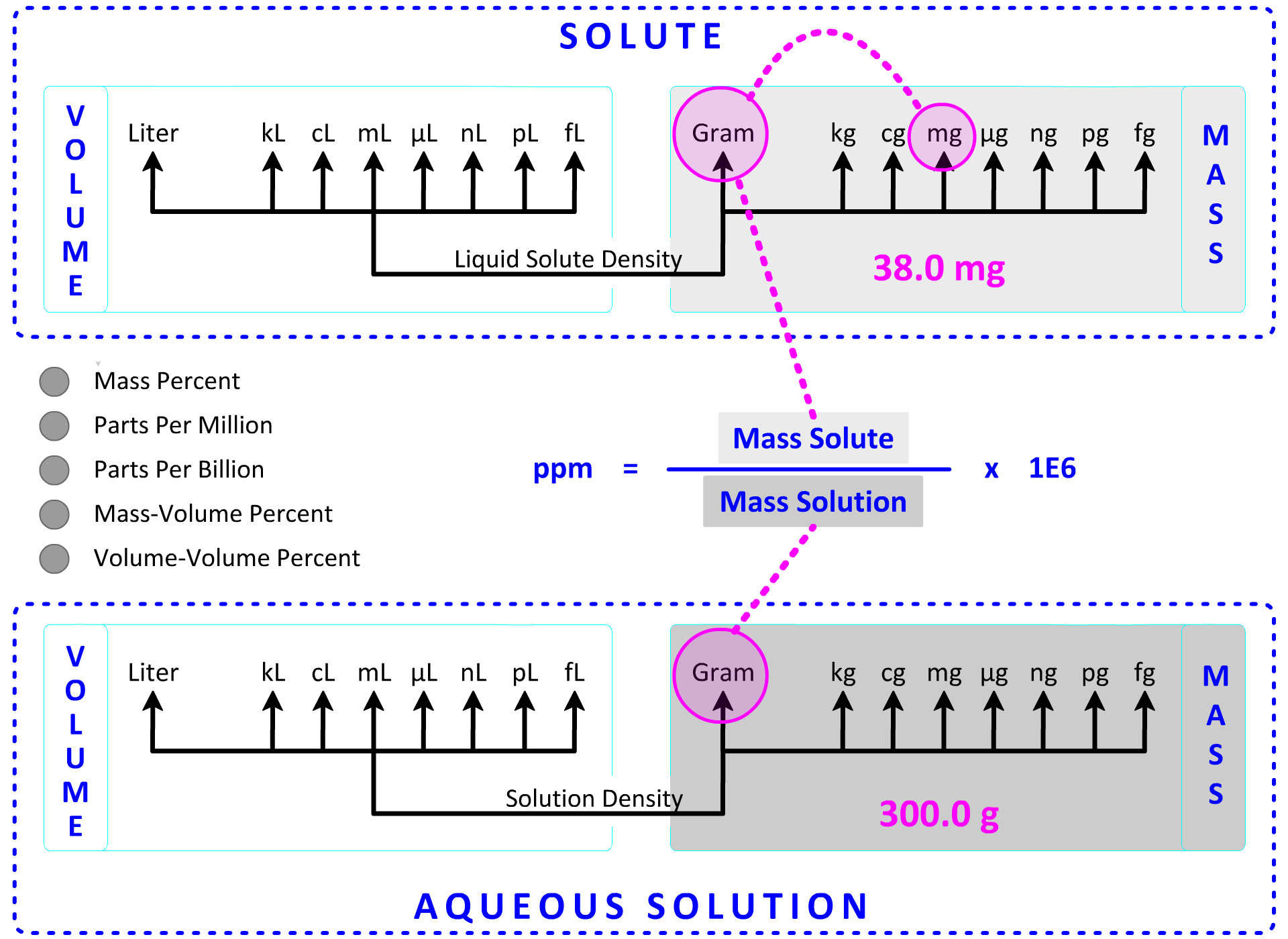
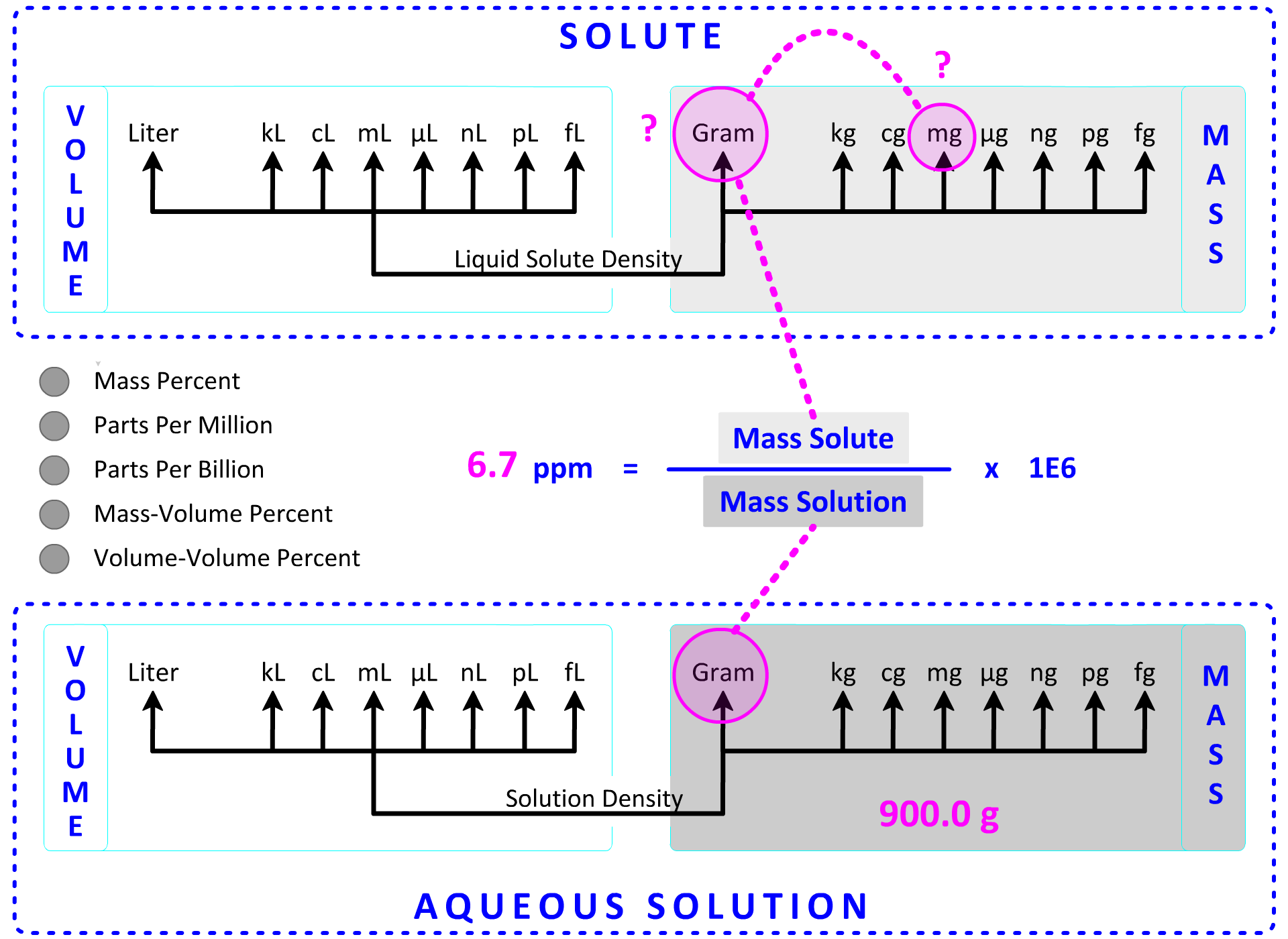
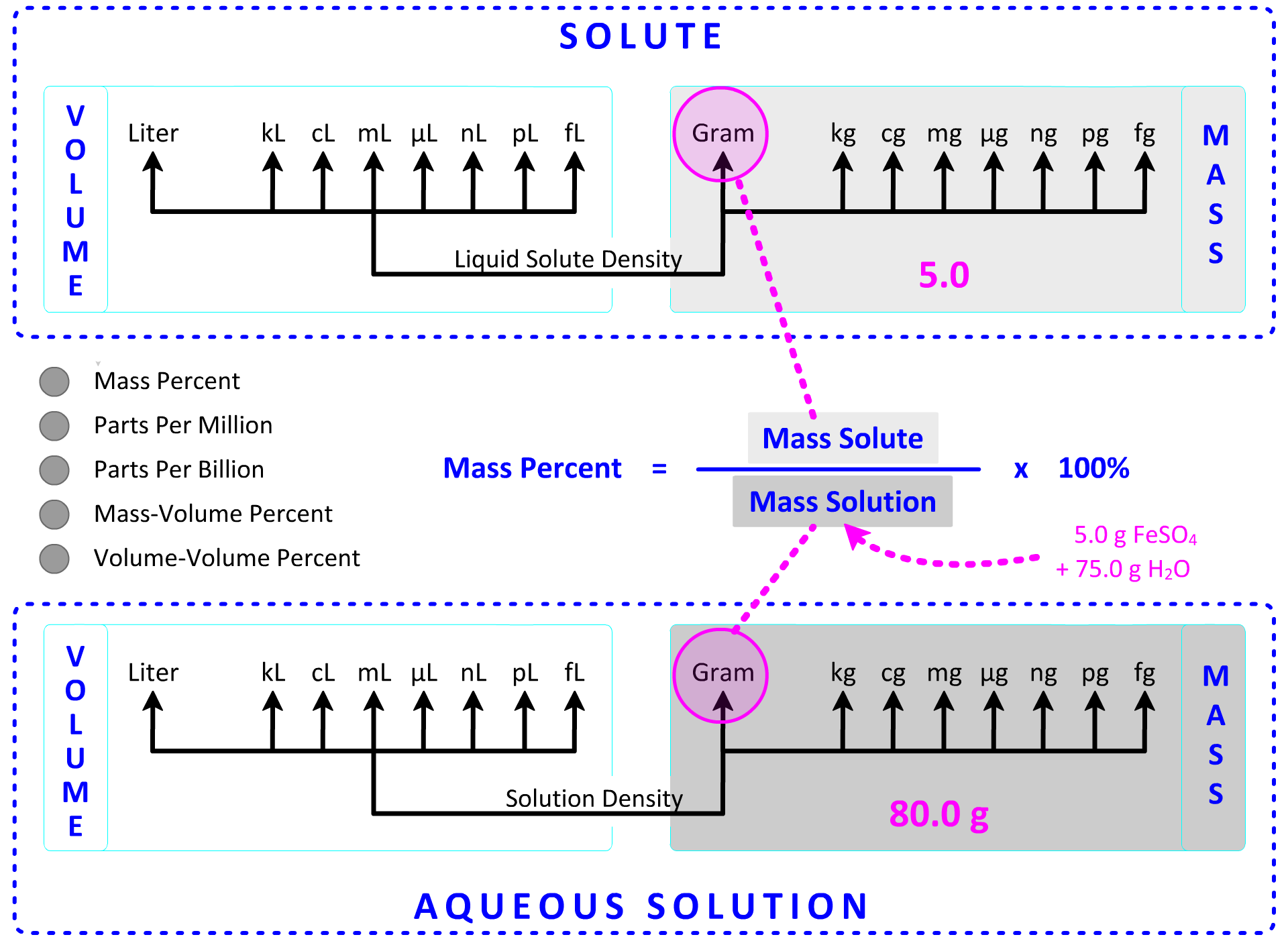
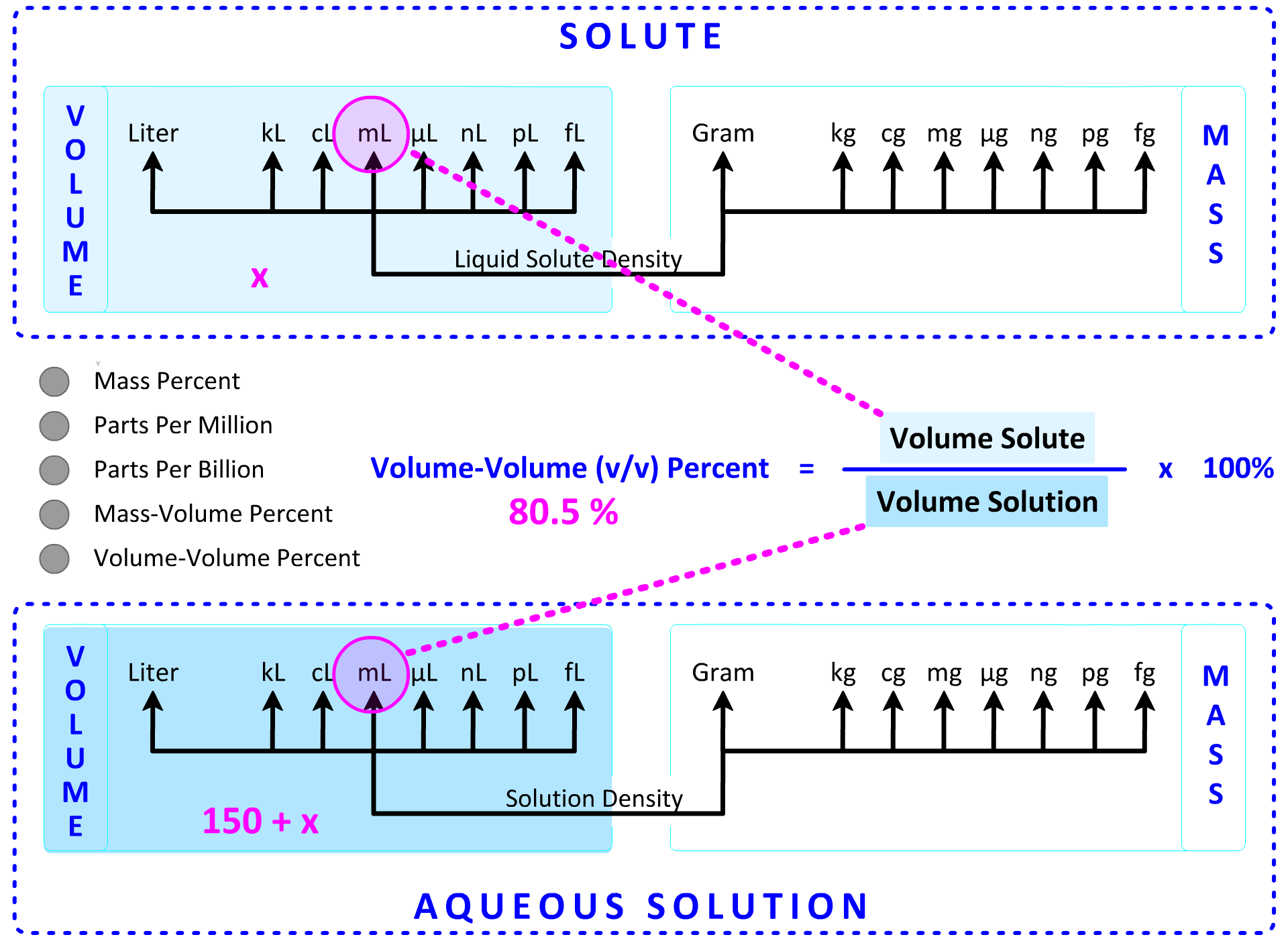
With previous calculations, we have used one of the Dimensional Analysis Maps as a calculation guide. In the last section, we added an Aqueous Solution Volume section and connected it to moles using Molarity as the conversion factor. While we could add an Aqueous Solution Mass section to include the concentration calculations presented above, an "inset map" of the sections in Map 3 that impact the five concentration expressions above is presented below. The top section contains mass and volume units for the solute while the bottom section contains mass and volume units for the solution. The solute, solvent and solution are bound by the following mathematical relationship:
Solute + Solvent = Solution
This relationship is 100% true for mass units (g solute + g solvent = g solution), but it is less reliable for volume units. The volume-based relationship becomes increasingly more reliable in very dilute solutions where concentrations are expressed in ppm and ppb. At this stage, we will assume the equation above is true for volume despite the limitations.
Activity: click the radio buttons to display the various concentration expressions . . . . observe that two of the four map sections are color-coded to the numerator and denominator for each concentration equation.
Activity: use the steps below to solve the following concentration problems
- Identify the values given as belonging to solute, solvent or solution.
- If a solvent value is given, add it to the solute value to calculate the solution value.
- Use the guide above to help you set up and solve the problem.
- After you have calculated the answer, check your setup by clicking the Show Setup link.
- If your setup is correct, check your answer by mousing over the pink area to the right of the "=" in Answer =
1. A sample of 300.0 g of drinking water is found to contain 38.0 mg Pb. What is this concentration in parts per million? Show Setup
2. A 900.0 g sample of sea water is found to contain 6.7 ppm Zn. How many mg of Zn are in the sea water? Show Setup
3. What is the percent by mass of 5.0 g of iron(II) sulfate dissolved in 75.0 g of water? Show Setup
4. An experiment requires a solution that is 80.5% methyl alcohol (CH3OH) by volume. What volume of methyl alcohol (in mL) is added to 150.0 mL of water to make this solution? Show Setup
5. What is the concentration in % m/v if 0.55 kg of solute is dissolved in water to make 1.5 L of solution? Show Setup